| Главная » Файлы » Необычные Люди и Животные |
Джон Милнор получил Абелевскую премию по математике
| 24.03.2011, 16:42 | |
Джон Милнор, профессор Института математических наук при Университете Стони-Брук, родился 20 февраля 1931 года. Через 20 лет, в 1951-м, он получил степень бакалавра в Принстонском университете и начал серьёзно заниматься наукой. Труды математика принесли ему всемирную известность, а сам он был награждён медалью Филдса и Национальной научной медалью США, получил премию Вольфа в области математики и три премии Лероя Стила от Американского математического общества.
Джон Милнор в 1963 году.
Перечислить все открытия, сделанные Джоном Милнором, едва ли возможно. Мы попробуем описать лишь одну его работу, которая считается наиболее важной и посвящена так называемым экзотическим сферам. Для начала рассмотрим одно из ключевых понятий математики — многообразие. Примером многообразия может служить поверхность Земли или тора: если вырезать совсем небольшой кусок такой поверхности, окажется, что его геометрия будет соответствовать привычной для нас евклидовой. Многообразие «в целом» такими свойствами не обладает; действительно, при движении из двух точек на экваторе в одном направлении — на север — пути должны встретиться, чего в обычной «двумерной» геометрии не произойдёт. Следует также заметить, что многообразия могут иметь любую размерность. В топологии многообразия, связанные взаимно-однозначным и непрерывным отображением, обратное к которому тоже непрерывно, считаются неразличимыми. Такие пространства называют гомеоморфными; обычно для иллюстрации гомеоморфизма используют поверхности куба и сферы или кружки и тора. 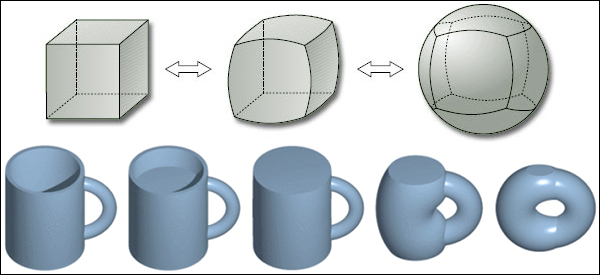 Дифференциальная геометрия рассматривает отображения другого типа, которые называют диффеоморфизмами. Последние должны быть взаимно-однозначными и дифференцируемыми. Из математического анализа известно, что понятия дифференцируемой и непрерывной (то есть не имеющей «скачков») функции не тождественны. Точнее, любая дифференцируемая в какой-то точке функция обязательно будет непрерывна в этой точке, но обратное утверждение ложно. Логично предположить, что правило действует и в нашем случае: диффеоморфные многообразия автоматически считаются гомеоморфными, тогда как последние диффеоморфными могут и не быть. Заслуга Джона Милнора заключается в том, что он нашёл первый пример пространств, эквивалентных с точки зрения топологии, но отличающихся друг от друга в рамках дифференциальной геометрии. В 1956 году учёный представил ту самую «экзотическую сферу» — гладкое многообразие, гомеоморфное семимерной сфере, но не диффеоморфное ей. Г-н Милнор также известен как талантливый популяризатор математики. «Его книга по теории Морса — эталон математической ясности и просто лучшая из всех прочитанных мною работ», — говорит сотрудник Рочестерского университета Дуглас Рейвнел (Douglas Ravenel). | |
| Просмотров: 1216 | Загрузок: 0 | | |
| Всего комментариев: 0 | |
